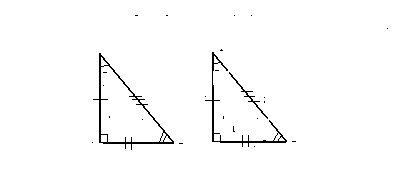ヒント1：三角形の型を決定する方法

科学

ヒント1：三角形の型を決定する方法

三角形は最も単純な多角形です。これは、1つの平面にある3つの点で構成されていますが、1つの直線ではなく、ペアごとにセグメントで結ばれています。しかしながら、三角形は全く異なることがあり、その結果、異なる特性を有することになる。

指示

6人を選抜するのは慣例である種三角形。この部門の中心には2つの分類があります：コーナーとサイドで。角度の種類別に分類すると、三角形を鋭く、四角形に、鈍角に分割することが想定されます。辺の比による分類は、三角形を汎用、等辺、二等辺三角形に分割する。各三角形は同時に2種類に属します。例えば、これは長方形であり、同時に多目的であり得る。

フォームの定義 三角形 コーナーの種類によって、非常に注意してください。鈍角の三角形が呼び出され、角の1つが鈍い、つまり90度を超えています。直角三角形は、1つの直接（90度に等しい）角度の存在によって計算することができます。ただし、三角形を鋭く分類するには、3つの角度すべてがシャープであることを確認する必要があります。

フォームの定義 三角形 辺の比率で、まずあなたはする必要がありますすべての3つの側面の長さを学ぶ。しかし、あなたが与えられていない脇の下の長さの条件によって、角度があなたを助けることができる場合。汎用性は三角形であり、三角形の三角形はすべて長さが異なります。辺の長さが未知である場合、3つの角度のすべてが異なる場合、三角形は汎用性があると分類できます。万能な三角形は、鈍角、長方形、鋭角にすることができます。

二等辺三角形、二等辺三角形3つの側面が互いに等しい。辺の長さがあなたに与えられていない場合は、2つの等しい角度で導かれます。多角形のような二等辺三角形は、鈍角でも、長方形でも鋭角でもあります。

同等のものにのみ名前を付けることができます3辺の長さが同じ三角形。すべての角度も互いに等しく、それぞれの角度は60度に等しい。したがって、正三角形は常に鋭角であることは明らかです。

ヒント2：鈍角と鋭角の三角形を特定する方法

最も単純なポリゴンは三角形です。それは、1つの平面に横たわる3つの点によって形成されるが、1つの直線上に横たわらず、セグメントによって対に接続される。それにもかかわらず、三角形は異なるタイプのものであり、したがって異なる特性を有する。

指示

3つのタイプの三角形を区別することが慣習的です：鈍い、鋭い、長方形。これは、角度の種類別の分類です。鈍角の三角形は、角の1つが鈍いものです。ブラントは角度であり、90度よりも大きいが、180度より小さい。例えば、三角形ABCでは、角度ABCは65°であり、角度BCAは95°であり、角度CABは20°である。角度ABCおよびCABは90°未満であるが、角度BCAが大きいので、三角形は鈍角である。

鋭い三角形は、すべてのアングルがシャープです。鋭い角度は、90度より小さく0度より大きな角度である。例えば、三角形ABCでは、角度ABCは60°であり、角度BCAは70°であり、角度CABは50°である。 3つの角度はすべて90°未満ですので、三角形は鋭角です。三角形のすべての辺が等しいことがわかっている場合、これはすべての辺の角度も同じですが、六角形に等しいことを意味します。したがって、そのような三角形内のすべての角度は90度未満であり、したがって、そのような三角形は鋭角である。

三角形の1つが90度に等しい場合、これは広角タイプまたは鋭角タイプには適用されないことを意味する。これは直角三角形です。

三角形の形が関係によって決定される場合当事者は、彼らは、等しく、多目的であり、二等辺三角形です。正三角形では、すべての辺が等しく、これは、あなたが見つけたように、三角形が鋭角であることを示します。三角形が2つの辺のみを有する場合、または辺が互いに等しくない場合、それは鈍角であり、長方形であり、鋭角であり得る。したがって、これらの場合、ポイント1,2または3に従って、角度を計算または測定し、推論を引き出す必要があります。

ヒント3：等しいと呼ばれる三角形

2つ以上の三角形の等価は、これらの三角形のすべての辺および角度が等しい場合に対応する。しかし、この同等性を証明するためのいくつかのより単純な基準があります。

あなたは必要になります

ジオメトリの教科書、紙のシート、シンプルな鉛筆、分度器、定規。

指示

あなたは、三角形の平等の兆候についてのパラグラフ。 2つの三角形の等価性を証明する多くの基本的な機能があることがわかります。等価性が検証された2つの三角形が任意である場合、それらのために3つの基本的な等号があります。三角に関する追加情報が分かっている場合は、主な3つの機能にいくつかの機能が追加されます。これは、例えば、直角三角形の等価性の場合に当てはまる。

平等についての最初のルールを読んでください三角形。ご存知のように、2つの三角形のいずれか1つの角と2つの隣接する辺が等しいことを証明できれば、三角形を等しく考えることができます。この法律の仕組みを理解するには、1つの点から出てくる2本の光線によって形成された2つの同じ定義された角度を分度器で紙面に描きます。どちらの場合も、描かれたコーナーの上から同じ側でルーラを測定します。分度器を使用して、形成された2つの三角形の角度を測定し、それらが等しいことを確認します。

このような実用性に頼らないために三角平等を理解するための手段は、平等の最初の兆候の証拠を読む。事実、三角形の平等に関する各規則は厳密な理論的証拠を持っており、規則を暗記するためにそれを使用するのは簡単ではない。

三角形の平等の2番目の記号を読んでください。このような三角形の片側と2つの隣接する角度が等しい場合、2つの三角形は等しくなると述べています。このルールを覚えておいて、三角形と2つの隣接する角の描画された面を想像してください。コーナーの辺の長さが徐々に長くなると想像してください。結局、それらは交差し、第3の角度を形成する。この精神的な課題では、精神的に増加している辺の交点とその結果の角度は、第三者と2つの隣接するコーナーによって一意的に決まることが重要です。

あなたがコーナーに関する情報を与えられていない場合三角形の等号の3番目の符号を使用します。このルールによれば、一方の3つの辺のすべてが他方の3つの辺に等しい場合、2つの三角形は等しいとみなされる。したがって、この規則は、三角形の辺の長さが三角形のすべての角度を一意的に決定するため、三角形自体を一意的に決定することを示しています。