ヒント1:対数から対数を取る方法
ヒント1:対数から対数を取る方法
対数を用いて指数を求める対数符号の下に示された数を導き出すための基礎が成立すべき程度。必ずしも対数の符号の下ではなく、数値でなければならない - 変数、多項式、関数などを指定することができる対数表現はもう1つの対数を含むことができます。特別な複雑さの対数から対数を計算する操作は、内部対数の変換によってしばしば単純化することができるので、特には示されない。
指示
1
それ自体、対数の対数を求める特別な変換はありません。ただ2つの操作を順番に実行するだけです。唯一の特徴は、内部対数で始まることである。他方の対数表現であるものからのものである。例えば、log3log2 512を探したい場合は、基底2(log2 512 = 9)の対数512を計算し、次に基底3(log3 9 = 2)で結果の対数を計算します。 log3 log2 512 = log3 9 = 2。
2
部分対数表現の1つが多項式の式は計算を進める前に、変換を使用しています。 logₐ(logᵤX +logᵤY)=logₐlogᵤ(のx * yを):例えば、同じ塩基による対数の和は、同じ理由で、それらの製品podlogarifmennyh式の対数に変換しました。同様に、対数との差を変換:logₐ(logᵤX - logᵤY)=logₐlogᵤ(X / Y)。
3
場合によっては、サブログ表現には数や変数を累乗して表現することで、表現をさらに単純化することが可能になります。例えば、第1のステップで使用されるlog3 log2 512の例は、以下の形式で表すことができる:log3 log2 29。これにより、内部対数の符号から9を導き出すことができ、log3log2 29 = log3(9 * log2)= log3(9 * 1)= 2であるため、対数512を計算する必要はなくなる。
4
前の手順で説明したルールは、根または分数を含む式からの対数に対しても適用されます。これを行うには、根を分数指数の形で想像してください。例えば、log3 log2√9√2を求める必要がある場合、√2は2の1/9の累乗で表すことができます。すると、log2÷9√2= 1/9 * log2 2 = 1/9 = 1/32 = 3-2となる。そしてlog3 3-2 = -2。これらの変換はすべて計算なしで行うことができ、解は以下のように書くことができた:log3 log2√3= log3(1/9 * log2)= log3(1/9)= log3(1/3)= log3 3-2 = -2。
ヒント2:数値の対数を求める方法
実際には、最も頻繁に使用されるのは10進数標準と呼ばれている対数、。特別なテーブルを構成し、それらを見つけるために、あなたが特定の精度で任意の正の数の対数の値を見つけることができた使用して、事前に標準フォームにそれを持って来ます。ほとんどの目的のために、0.0001に、仮数対数を含んで十分Bradis 4テーブルのアップです。特徴は、簡単に数の1種類で見つけることができます。非常にシンプルなテーブルの取り扱い。
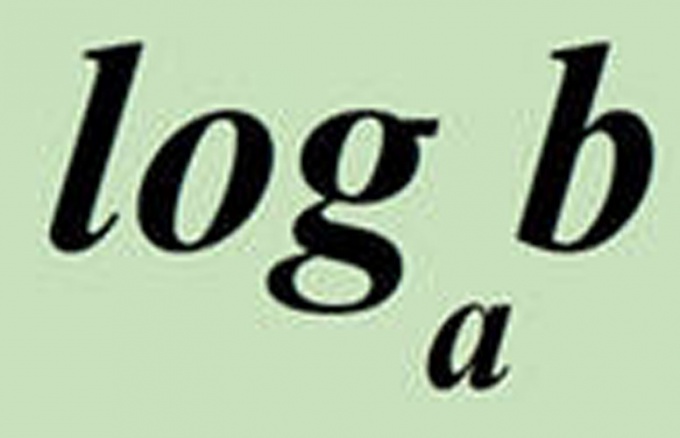
あなたは必要になります
- - 対数の1つの基底から別の基底への遷移の式。
- - Bradysの4桁の数学的な表。
指示
1
基数が10でない場合は、対数を標準ビューにしておきます。ある基底から別の基底への遷移式を使用します。
2
対数の特性を求める。 数値が1以上の場合は、指定された数値の整数部分の桁数を数えます。この数量からユニットを取り出し、特性値を取得します。たとえば、対数が56.3の場合、特性は1です。数値が1未満の小数点以下の場合は、その中の0の数を最初の非ゼロの桁に数えます。特性の値を負にします。たとえば、0.0002の対数の場合、特性は-4です。
3
仮数を求めるための数を全体この番号ではカンマを無視し、番号の末尾にすべてのゼロを捨てます。 10進数と最後の0のコンマの位置は、仮数の値に影響しません。整数を書き留めます。たとえば、56.3の対数は563です。この数値に含まれる桁数によっては、4桁の表を扱うアルゴリズムが異なります。アルゴリズムには3種類あります。
4
以下を実行して対数の仮数を求めるアクションは、その場所の番号が3桁である場合。 XIII«仮数の対数4桁の数表Bradisテーブルを検索します。」最初の列«N»仮数が求められているに番号の最初の2桁を含む行に移動します。それは元の数の3桁目と一致する数の列と交差するまで、我々は、数563を持っている場合、例えば、最初の列が56の価値がある行を探し、右への行に継続します。この例では、マッチした文字列と列の交点に列番号3は、仮数の値です。 563の数に見出さ仮数は0.7505に等しいです。
5
以下を実行して対数の仮数を求める見つかった番号が2桁または1桁の場合は、アクション。属性は精神的にはこのような数の0になり、3値になります。その数が56であれば、560が得られ、得られた3桁の数字から仮数を見つける。これを行うには、手順4の手順に従います。番号560の仮数は0.7482です。
6
以下を実行して対数の仮数を求める見つかった番号が4桁の場合は、アクション。与えられた数の最初の3桁で表される数の仮数を求めます。これを行うには、手順4の手順を実行します。次に、見つかった仮数から、テーブルの右側の、垂直グリース線の後ろにあり、4桁目の訂正を含む水平線に沿って移動します。修正領域で、番号の4桁目と一致する番号の列を探します。行と列の交点に3桁の数字が示す仮数部に修正を加える。例えば、仮数を見つけるための数が5634である場合、563の仮数は0.7505である。図4の補正は3です。最終結果は0.7508です。
7
以下を実行して対数の仮数を求めるそれに4桁以上の数字が含まれていると数字を4文字に丸めて、5桁目から始まるすべての数字がゼロになるようにします。最後の0を削除し、4桁の数字で仮数を見つけます。これを行うには、手順7の手順を実行します。
8
特性の仮数と仮数の和として、数の対数を求めます。考察中の例では、56.3の対数は1.7505である。
ヒント3:対数を見つける方法
対数 基数aを有する数xは、a y = xとなるような数yである。対数は非常に多くの実用的な計算を容易にするので、それらを使用できることが重要です。

指示
1
基底aに対する数xの対数はloga(x)で表される。たとえば、log2(8)は底2の8の対数です.2 ^ 3 = 8なので、3です。
2
対数は正の数に対してのみ定義されます。負の数とゼロには、基底にかかわらず、対数はありません。この場合、対数自体は任意の数にすることができます。
3
対数の底は任意でよい1を除く正の数。しかしながら、実際には、2つの塩基が最も頻繁に使用される。基数10の対数は10進数と呼ばれ、lg(x)で表されます。実数計算では、小数点の対数が最も頻繁に見られます。
4
対数の第2の一般的な基礎 - 非理性の超越数e = 2.71828 ...基底eの対数は自然と呼ばれ、ln(x)で表されます。関数e ^ xとln(x)は、微分積分には重要な特殊な性質を持っているため、自然対数は数学的分析でより頻繁に使用されます。
5
2つの数の積の対数は、loga(x * y)= loga(x)+ loga(y)である。 log2(256)= log2(32)+ log2(8)= 8.特定の2つの数値の対数は、loga(x / y)= loga(x)-loga(y)の差に等しくなります。
6
で構築された数の対数を求めるには次数の対数を指数で掛ける必要があります。loga(x ^ n)= n * loga(x)指数は、正、負、ゼロ、整数、または小数の任意の数にすることができます。任意のxに対してx ^ 0 = 1なので、任意のaに対してloga(1)= 0です。
7
対数は、加算、勃起による乗算を置き換えます乗算の力と、除算による根の抽出とに分けられる。表に含まれていない数の対数を求めるには、対数が表にある2つ以上の数の積として表現し、これらの対数を加算して最終結果を求める必要があります。
8
自然を簡単に計算する方法対数 - 級数にこの機能の拡張を使用します。ln(1 + X)= Xの - (X ^ 2)/ 2 +(x ^ 3)/ 3 - (X ^ 4)/ 4 + ... +((-1) ^(N + 1))*((X ^ N)/ N)は数がため-1 <X≤1値LN(1 + X)を得る.This。換言すれば、このシリーズの外部2.自然対数番号に(0を含まない)0からの生成物の対数は、対数の和であることを利用して見出さ合計することによって求めることができる数の自然対数を計算することが可能です。特定のLN(2×)= LN(X)+ LN(2)です。
9
実用的な計算のためには、時に便利です自然対数から小数点まで移動します。 log10(x)= ln(x)/ ln(10)このようにして、log10(x)= logn(x)/ loga(b)となる。