LovesTheTeam.com

指示

1

円はポリゴンに内接すると呼ばれ、説明図の各側の共通点がある場合。ポリゴン内の内接円の中心は常に、その内角の二等分線の交点にあります。円の半径、π - - 番号「PI」 - 数学定数等しい3,14.Dlya円半径接線の点に中心からの間隔に等しい幾何学図形に内接する円で囲まれた領域は、Rは、式S =π* R2、によって定義されます党の図面と。これにより、ポリゴンに内接する円の半径とポリゴンのパラメータによって記述図形発現面積円の要素間の関係を決定することが可能です。

2

いずれの三角形でも、一意のr =sΔ/pΔここで、rは内接円の半径、sΔは三角形の面積、pΔは三角形の半分の直径です。得られた半径の値を、三角形の円周に沿って記述された要素を介して円の面積の式に代入して代入する。次に、面積sΔおよび半値pΔを有する三角形に内接する円の面積Sを、S =π*（sΔ/pΔ）2の式で計算する。

3

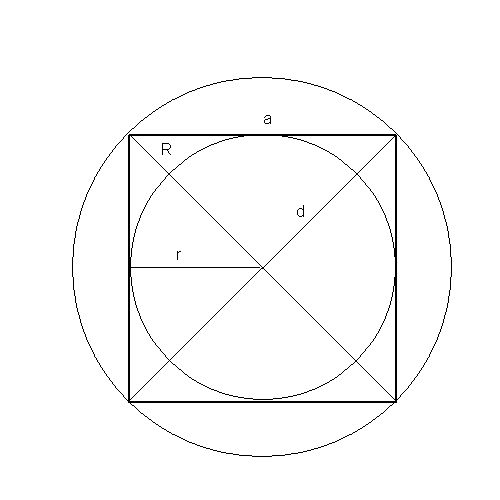
S =π* a2 / 4は、aの四角形に内接する円の面積SがS =π* a2 / 4である。

4

菱形では、内接円の面積Sは、 Sは、=π*（d₁d₂/ 4A）²。 - 台形の高さS =π*（H / 2）²、H： - 菱形の対角線、及び - この式d₁とd₂に側S romba.Dlya台形領域そこ式によって定義される円周に内接。

5

正六角形のa面は円の面積Sは、S =π*a²の式で計算されます。円は、任意の数の辺を持つ正多角形に内接することができます。辺aと辺数n：r = a / 2tg（360°/ 2n）の多角形に内接する円の半径rを求める一般的な式。このような多角形に内接する円の面積Sは、S =π*（a / 2tg（360°/ 2n）2/2）である。